이 글이 도움되셨다면 광고 클릭 부탁드립니다 : )
이번 포스팅에서는 anomaly탐지를 위한 오토인코딩을 활용한 GMM논문을 간략하게 리뷰해보고 Kaggle의 Credit Card Data에 실습해보겠습니다.
Deep Autoencoding Gaussian Mixture Model for Unsupervised Anomaly Detection(DAGMM) 논문은 링크에 걸어두었고 구현된 코드는 구글에 치면 여러가지가 나오는데 credit card data를 활용한 github를 첨부해두었습니다.
논문 리뷰에 앞서 GMM에 대해 간략하게 알아보겠습니다.
0. GMM이란?
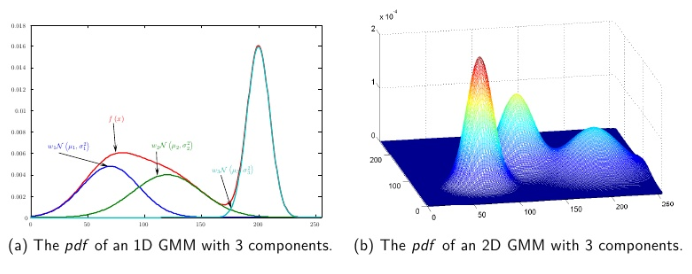
Gaussian Mixture Model(GMM)은 이름에서 알 수 있듯이 가우시안 분포가 혼합된 모델로 Clustering하는 방법입니다. 군집의 수 k는 따로 정해주어야 하며 정해진 k에 따라 복잡한 형태의 분포를 k개의 gaussian 분포로 쪼개어 줍니다. k개의 gaussian 분포의 parameter($ \pi, \mu, \Sigma $)는 EM알고리즘으로 추정합니다. 여기서 $ \pi_k $는 각 관찰치가 k번째 군집에 포함될 학률, $ \mu_k $와$ \Sigma_k $는 k번째 군집의 평균과 분산이 됩니다.
EM알고리즘(참고)은 (1) Expectation Step에서 log-likelihood값의 평균을 구하고 (2) Maximization Step에서 log-likelihood를 최대화하는 parameter를 추정하고 log-likelihood의 변화량이 적을 때 학습을 멈춥니다.
GMM 리뷰는 여기까지하고 DAGMM에 대해 알아보겠습니다.
1. Introduction
수많은 이상치 탐지 방법들이 있지만, 입력 데이터의 차원이 증가할 수록 원 자료상에서 밀도를 추정하는 것이 어려워지고, 모든 입력 데이터가 나타날 확률이 굉장히 적아서 이상치로 잘못 판단할 수 있습니다.
이러한 문제를 해결하기 위해 일반적으로 2단계 접근방법(차원 축소 후, 밀도 추정)을 많이 사용하는데, 1단계에서 하는 차원 축소는 2단계 밀도 추정에 대한 어떠한 정보도 인식하지 못하기 때문에, 이상치 탐지에 꼭 필요한 정보가 차원 축소 단계에서 사라질수 있다는 문제점이 있습니다.
이에 최근(16년) 연구들에서 DNN을 활용해 차원 축소와 밀도 추정을 동시에 진행하는 방법론을 연구하였지만, 원 데이터에서의 중요 정보를 저 차원의 축소된 공간에서 유지할 수 없었고, 단순한 밀도 추정 모형을 사용해 밀도함수를 정확히 추정하기가 힘들었습니다.
따라서 본 논문에서는 비지도 이상치 탐지를 위해 앞에서 언급한 어려움들을 해결하는 DAGMM을 소개합니다.
2. DAGMM
2.1 특징
DAGMM의 특징은 다음과 같습니다.
첫 번째, DAGMM은 오토인코더를 사용하여 축소된 차원과 복원 오차에 대한 특성을 유지하여 입력값의 중요 정보를 저차원상에서도 잘 유지합니다.
두 번째, DAGMM은 학습된 저차원의 공간에서 GMM을 활용하여 복잡한 구조를 가진 입력 데이터에 대한 밀도 함수 추정하여 밀도 추정에 강력한 성능을 보입니다.
세 번째, DAGMM은 end-to-end 학습에 적합합니다. 일반적으로 end-to-end 학습으로 deep autoencoder를 학습시키면 local optima로 빠지기 쉬운데 DAGMM은 GMM단계에서 생기는 정규화로 local-optima로 빠지지 않는 것을 실험을 통해 확인했습니다.
2.2 구조
DAGMM은 두개의 주요 요소인 압축 네트워크, Compression network(autoencoder)와 추정 네트워크, Estimation network(GMM)로 구성됩니다.
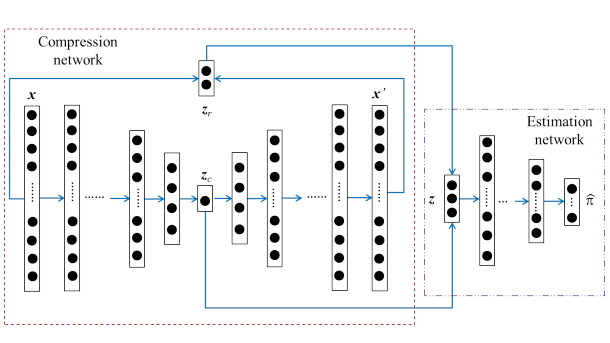
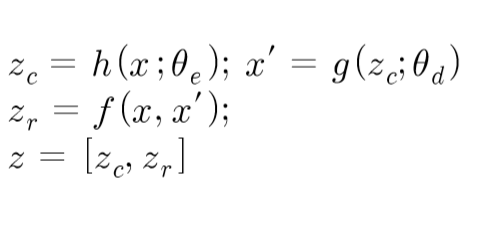
2.2.1 압축 네트워크
압축 네크워트에서는 deep autoencoder를 사용하여 입력 데이터의 차원을 축소합니다.
$ Z_c $는 차원축소를 통해 축소된 저 차원의 데이터이고 $ Z_r $은 원 데이터와 복원 데이터의 오차에서 파생된 변수들입니다. $ Z_r $는 여러차원으로 설정할 수 있는데, 예를 들어 유클리딘언 거리, 코사인 유사도 등 복원 오차에 대한 특성을 여러 차원으로 정의할 수 있다.
2.2.2 추정 네트워크
추정 네트워크에서는 차원 축소된 데이터를 입력값으로 하여, GMM으로 밀도 추정을 합니다.(k 설정해줘야함)
밀도 추정을 위해 multi-layer 인공신경망을 이용하여 각 표본의 혼합 분포를 예측하고 parameter를 추정합니다. 그다음 추정된 parameter를 사용하여 sample energy를 계산하여 어떤 기준값보다 큰 energy를 갖는 데이터를 비정상 자료로 분류합니다.
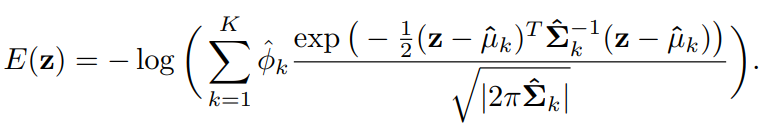
2.2.3 목적함수(objective function)
DAGMM의 학습을 위한 목적함수는 세 가지로 구성됩니다.
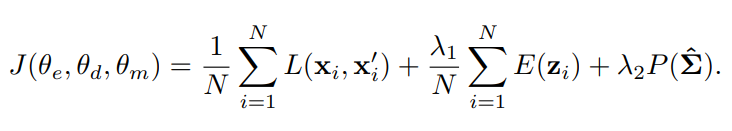
1. 복원 오차를 최소화(L2-norm)
2. sample energy를 최소화, likelihood(가능도)를 최대화
3. 공분산 행렬에 벌점화 함수 추가(singularity 문제... 대각 성분이 0이 되면 무의미한 trival 해를 가짐)
3. Experimental Results
(자세한 내용은 논문 참고)
3.1 검증 데이터
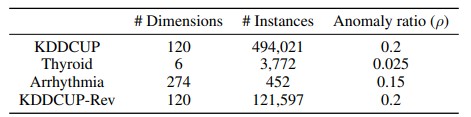
3.2 검증 결과
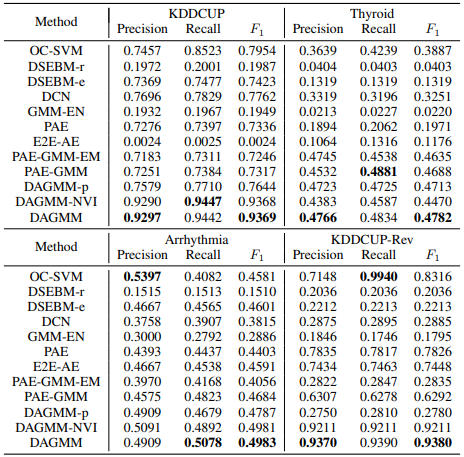
4. 구현 코드
import os
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
# download this Kaggle dataset from: https://www.kaggle.com/mlg-ulb/creditcardfraud
FILE_PATH = "c:/Credit_Card_Fraud_Data/"
csv_path = os.path.join(FILE_PATH, "kaggle_fraud_data.csv")
df = pd.read_csv(csv_path)
# number of features = 30 (features, incl. time) + 1 (label)
df = df.drop(['Time'], axis=1) #drop time feature; number of input features = 29
'''
# normalize data below
cols_to_norm = ['V1','V2','V3','V4','V5','V6','V7','V8','V9','V10',
'V11','V12','V13','V14','V15','V16','V17','V18','V19','V20',
'V21','V22','V23','V24','V25','V26','V27','V28', 'Amount' ]
df.loc[:, cols_to_norm] = (df[cols_to_norm] - df[cols_to_norm].mean()) / df[cols_to_norm].std()
'''
cols_to_norm = ['Amount' ]
df.loc[:, cols_to_norm] = (df[cols_to_norm] - df[cols_to_norm].mean()) / df[cols_to_norm].std()
df.head()
#df.info()
df.describe()
cc_data = df.values #convert pandas dataframe to numpy array
cc_data.shape # shape -> (284807, 30)
print("cc_data.shape=", cc_data.shape)
#cc_data_normal = cc_data[cc_data[:,30]==0] #with 'Time'
#cc_data_fraud = cc_data[cc_data[:,30]==1]
cc_data_normal = cc_data[cc_data[:,29]==0] #without 'Time'
cc_data_fraud = cc_data[cc_data[:,29]==1]
print("shape cc_data_normal", cc_data_normal.shape) #shape -> (284315, 31) normal examples
print("shape cc_data_fraud", cc_data_fraud.shape) #shape -> (492, 31) fraud examples
from sklearn.model_selection import train_test_split
# without Time feature
train_total_data_normal, test_total_data_normal, y_train_normal, y_test_normal = train_test_split(
cc_data_normal, cc_data_normal[:,29], test_size=0.2, random_state=37)
#############################################################################################
import sklearn
import sklearn.pipeline
import sklearn.preprocessing
###############################################################
#expects input state shape = (batch_dim,2)
#returns output 'scaled' shape = (batch_dim,2)
def process_state(state):
scaled = scaler.transform(state)
return scaled
#################################################################
print("shape train_total_data_normal", train_total_data_normal.shape)
total_training_instances = len(train_total_data_normal)
print(total_training_instances)
test_total_data = np.concatenate((cc_data_fraud, test_total_data_normal), axis=0)
print("shape test_total_data", test_total_data.shape)
#n_epochs = 50
#z_dim = 1 #1 #z compression dimensionality
#K_dims = 3 # orig 3
#lamda1 = 0.1
#lamda2 = 0.01 # 0.01
#lr = 0.001 #0.001
#batch_size = 1024 # 256, 512, 1024
def dagmm(n_epochs=100, hp_drop=0.4, z_dim=1,K_dims=3,lamda1=0.1,lamda2=0.01,lr=0.001,
batch_size=1024, n_hidden1=20, n_hidden2=10, n_hidden3=5, n_layer1=10):
#######################################################################################
import tensorflow as tf
import numpy as np
from scipy.optimize import minimize_scalar
tf.reset_default_graph()
training = tf.placeholder_with_default(False, shape=())
def encoder(x, z_dim, n_hidden1, n_hidden2, n_hidden3, dropout_prob):
with tf.variable_scope("encoder"):
init_xavier = tf.contrib.layers.xavier_initializer()
he_init = tf.contrib.layers.variance_scaling_initializer()
x_drop = tf.layers.dropout(x, dropout_prob, training=training)
hidden1 = tf.layers.dense(x_drop, n_hidden1, tf.nn.tanh, he_init)
hidden1_drop = tf.layers.dropout(hidden1, dropout_prob, training=training)
hidden2 = tf.layers.dense(hidden1_drop, n_hidden2, tf.nn.tanh, he_init)
hidden2_drop = tf.layers.dropout(hidden2, dropout_prob, training=training)
hidden3 = tf.layers.dense(hidden2_drop, n_hidden3, tf.nn.tanh, he_init)
hidden3_drop = tf.layers.dropout(hidden3, dropout_prob, training=training)
z_comp = tf.layers.dense(hidden3_drop,z_dim,None, he_init)
return z_comp
def decoder(z_comp, x_dim, n_hidden1, n_hidden2, n_hidden3, dropout_prob, reuse=False):
with tf.variable_scope("decoder"):
init_xavier = tf.contrib.layers.xavier_initializer()
he_init = tf.contrib.layers.variance_scaling_initializer()
hidden3 = tf.layers.dense(z_comp, n_hidden3, tf.nn.tanh, he_init)
hidden3_drop = tf.layers.dropout(hidden3, dropout_prob, training=training)
hidden2 = tf.layers.dense(hidden3_drop, n_hidden2, tf.nn.tanh, he_init)
hidden2_drop = tf.layers.dropout(hidden2, dropout_prob, training=training)
hidden1 = tf.layers.dense(hidden2_drop, n_hidden1, tf.nn.tanh, he_init)
hidden1_drop = tf.layers.dropout(hidden1, dropout_prob, training=training)
x_hat_logits = tf.layers.dense(hidden1_drop, x_dim, None, he_init)
#x_hat_sigmoid = tf.sigmoid(x_hat_logits)
return x_hat_logits
def estimation_network(z_concat, K_dims, n_layer1, dropout_prob_paper):
n_softmax=K_dims
with tf.variable_scope("estimation"):
init_xavier = tf.contrib.layers.xavier_initializer()
he_init = tf.contrib.layers.variance_scaling_initializer()
layer1 = tf.layers.dense(z_concat, n_layer1, tf.nn.tanh, he_init)
layer1_drop = tf.layers.dropout(layer1, dropout_prob_paper, training=training)
gamma = tf.layers.dense(layer1_drop, n_softmax, tf.nn.softmax, he_init)
return gamma
def compression_autoencoder(x, x_dim, z_dim, n_hidden1, n_hidden2, n_hidden3, dropout_prob):
z_comp = encoder(x, z_dim, n_hidden1, n_hidden2, n_hidden3, dropout_prob)
x_hat = decoder(z_comp, x_dim, n_hidden1, n_hidden2, n_hidden3, dropout_prob)
ae_loss = tf.reduce_mean(tf.squared_difference(x,x_hat))
recon_error = x - x_hat
#cos_similarity and recon_norm are shape = (batch_size,)
recon_error_magnitude = tf.norm(
recon_error, ord='euclidean', axis=1, keep_dims=True) #tensor of shape (batch_size, 1)
x_unit = tf.nn.l2_normalize(x, dim=1)
x_hat_unit = tf.nn.l2_normalize(x_hat, dim=1)
cos_similarity=tf.reduce_sum(
tf.multiply(x_unit ,x_hat_unit),axis=1,keep_dims=True) #shape = (batch_size,1)
return z_comp, x_hat, ae_loss, recon_error_magnitude, cos_similarity
def density_parameters(gamma, z):
#gamma expected shape-> (N,K)
#z expected shape-> (N, z_dim)
phi = tf.reduce_mean(gamma, axis=0) #shape phi= (K,)
gamma_expand = tf.expand_dims(gamma, axis=-1) #gamma_expand -> (N,K,1)
z_expand = tf.expand_dims(z, axis=1) #z_expand -> (N,1,3)
gamma_z = tf.matmul(gamma_expand,z_expand) #out_shape =(N,K,1)x(N,1,3)=(N,K,3) for z_dim = 3
mu_numerator = tf.reduce_sum(gamma_z, axis=0) #shape = (K,3)
mu_denominator = tf.expand_dims(tf.reduce_sum(gamma, axis=0), axis=-1) #shape = (K,1)
mu = mu_numerator / mu_denominator #mu shape->(K,3)
#######################################################
#Co-variance:
z_expand = tf.expand_dims(z, axis=1) #output shape=(N=2,1,3)
mu_expand = tf.expand_dims(mu, axis=0) #output shape=(1,4,3)
z_minus_mu = tf.subtract(z_expand, mu_expand) #output shape=(N=2,4,3)
z_minus_mu_expand_left = tf.expand_dims(z_minus_mu, axis=2) #shape=(N=2,4,1,3)
z_minus_mu_expand_right = tf.expand_dims(z_minus_mu, axis=-1) #shape=(N=2,4,3,1)
z_mu_outer_product = tf.matmul(z_minus_mu_expand_right, z_minus_mu_expand_left)
gamma_double_expand = tf.expand_dims(tf.expand_dims(gamma, axis=-1), axis=-1)
gamma_x_outer_product = gamma_double_expand * z_mu_outer_product
covariance_numerator = tf.reduce_sum(gamma_x_outer_product, axis=0) #shape=(K=4,3,3)
g_expand = tf.expand_dims(tf.expand_dims(tf.reduce_sum(gamma, axis=0), axis=-1), axis=-1)
covariance_final = covariance_numerator / g_expand #final covariance term shape=(4,3,3)
return phi, mu, covariance_final
def energy_density(z, phi, mu, covariance, z_dim, K_dims):
z_expand = tf.expand_dims(z, axis=1) #output shape=(N=2,1,3)
mu_expand = tf.expand_dims(mu, axis=0) #output shape=(1,4,3)
z_minus_mu = tf.subtract(z_expand, mu_expand) #output shape=(N=2,4,3)
z_minus_mu_expand_left = tf.expand_dims(z_minus_mu, axis=2) #output shape=(N=2,4,1,3)
z_minus_mu_expand_right = tf.expand_dims(z_minus_mu, axis=-1) #output shape=(N=2,4,3,1)
total_z_dim = z_dim + 2
dummy_matrix = tf.eye(
num_rows = total_z_dim, num_columns = total_z_dim, batch_shape = [K_dims], dtype=tf.float32)
eps = 2.0e-12
eps_matrix = dummy_matrix * eps
covariance = tf.add(covariance, eps_matrix)
covariance_inverse = tf.matrix_inverse(covariance) #input and output shape = (4,3,3)
cov_inverse_expand = tf.expand_dims(covariance_inverse, axis=0) #output shape=(1,4,3,3)
cov_inverse_tiled = tf.tile(cov_inverse_expand, [tf.shape(z)[0],1,1,1]) #output shape=(?,4,3,3)
z_mu_x_cov_inverse = tf.matmul(
z_minus_mu_expand_left, cov_inverse_tiled) #output shape=(2,4,1,3)
z_mu_cov_inv_z_mu = tf.matmul(
z_mu_x_cov_inverse, z_minus_mu_expand_right) #output shape=(2,4,1,1)
exp_term = tf.exp(-0.5 * z_mu_cov_inv_z_mu)
phi_expand = tf.expand_dims(tf.expand_dims(phi, axis=-1),axis=-1)
phi_exp_product = phi_expand * exp_term
phi_exp_product_squeeze = tf.squeeze(phi_exp_product)
energy_divided_by = tf.expand_dims(
tf.sqrt(2.0 * 3.14159 * tf.matrix_determinant(covariance)),axis=0) + 2.0e-12
term_to_be_summed = phi_exp_product_squeeze / tf.squeeze(energy_divided_by)
term_inside_log = tf.reduce_sum(term_to_be_summed, axis=1) + 2.0e-12
energy = -1.0 * tf.log(term_inside_log)
final_energy = tf.expand_dims(energy, axis=-1) #ouptut shape=(?=batch_size,1)
return final_energy
def test_energy(z, phi_test, mu_test, covariance_test, z_dim, K_dims):
#data_tf = tf.convert_to_tensor(data_np, np.float32)
#convert Numpy numerical value arrays to TF tensor objects
phi = tf.convert_to_tensor(phi_test, np.float32)
mu = tf.convert_to_tensor(mu_test, np.float32)
covariance = tf.convert_to_tensor(covariance_test, np.float32)
total_z_dim = z_dim + 2
dummy_matrix = tf.eye(
num_rows = total_z_dim, num_columns = total_z_dim, batch_shape = [K_dims], dtype=tf.float32)
eps = 2.0e-12
eps_matrix = dummy_matrix * eps
covariance = tf.add(covariance, eps_matrix)
z_expand = tf.expand_dims(z, axis=1) #output shape=(N=2,1,3)
mu_expand = tf.expand_dims(mu, axis=0) #output shape=(1,4,3)
z_minus_mu = tf.subtract(z_expand, mu_expand) #output shape=(N=2,4,3)
z_minus_mu_expand_left = tf.expand_dims(z_minus_mu, axis=2) #output shape=(N=2,4,1,3)
z_minus_mu_expand_right = tf.expand_dims(z_minus_mu, axis=-1) #output shape=(N=2,4,3,1)
covariance_inverse = tf.matrix_inverse(covariance) #input and output shape = (4,3,3)
cov_inverse_expand = tf.expand_dims(
covariance_inverse, axis=0) #output shape = (1,4,3,3)
cov_inverse_tiled = tf.tile(
cov_inverse_expand, [tf.shape(z)[0],1,1,1]) #output shape=(?,4,3,3)
z_mu_x_cov_inverse = tf.matmul(
z_minus_mu_expand_left, cov_inverse_tiled) #output shape=(2,4,1,3)
z_mu_cov_inv_z_mu = tf.matmul(
z_mu_x_cov_inverse, z_minus_mu_expand_right) #output shape=(2,4,1,1)
exp_term = tf.exp(-0.5 * z_mu_cov_inv_z_mu)
phi_expand = tf.expand_dims(tf.expand_dims(phi, axis=-1),axis=-1)
phi_exp_product = phi_expand * exp_term
phi_exp_product_squeeze = tf.squeeze(phi_exp_product)
energy_divided_by = tf.expand_dims(
tf.sqrt(2.0 * 3.14159 * tf.matrix_determinant(covariance)),axis=0) + 1.0e-12
term_to_be_summed = phi_exp_product_squeeze / tf.squeeze(energy_divided_by)
term_inside_log = tf.reduce_sum(term_to_be_summed, axis=1) + 1.0e-12
energy = -1.0 * tf.log(term_inside_log)
final_energy_test = tf.expand_dims(energy, axis=-1) #ouptut shape=(?=batch_size,1)
return final_energy_test
#############################################
from sklearn.metrics import precision_recall_fscore_support as prf, accuracy_score
def f1(thresh, energy_array, labels):
prediction = (energy_array>thresh).astype(int)
pred = prediction.reshape(-1)
gt = labels.astype(int)
accuracy = accuracy_score(gt,pred)
precision, recall, f_score, support = prf(gt, pred, average='binary')
return -f_score
#######################################################################################
x_dim = 29 #with Time dropped there are 29 input features
dropout_prob = tf.placeholder(tf.float32, name='dropout_prob')
dropout_prob_paper = tf.placeholder(tf.float32, name='dropout_prob_paper')
x = tf.placeholder(tf.float32, shape=[None, x_dim])
z_comp, x_hat, ae_loss, recon_error_magnitude, cos_similarity = compression_autoencoder(
x, x_dim, z_dim, n_hidden1, n_hidden2, n_hidden3, dropout_prob)
z_concat = tf.concat([z_comp, recon_error_magnitude, cos_similarity ], axis=1)
gamma = estimation_network(z_concat, K_dims, n_layer1, dropout_prob_paper)
phi, mu, covariance = density_parameters(gamma, z_concat)
energy = energy_density(z_concat, phi, mu, covariance, z_dim, K_dims)
energy_loss = tf.reduce_mean(energy)
indices = [[k_index, j_index, j_index] for k_index in range(K_dims)
for j_index in range(z_dim + 2)]
#indices = [[0,0,0], [0,1,1], [0,2,2], [1,0,0], [1,1,1],
#[1,2,2], [2,0,0], [2,1,1], [2,2,2], [3,0,0], [3,1,1], [3,2,2]]
cov_loss = tf.gather_nd(covariance, indices)
cov_loss_reciprocal = 1 / cov_loss
P_Sigma_loss = tf.reduce_sum(cov_loss_reciprocal)
total_loss = ae_loss + lamda1*energy_loss + lamda2*P_Sigma_loss
t_vars = tf.trainable_variables()
all_training_vars = [var for var in t_vars if "encoder" or "decoder" or "estimation" in var.name]
training_op = tf.train.AdamOptimizer(lr).minimize(total_loss, var_list=all_training_vars)
number_of_batches = int(total_training_instances / batch_size)
with tf.Session() as sess:
sess.run(tf.global_variables_initializer(),
feed_dict={dropout_prob : hp_drop, dropout_prob_paper : hp_drop})
for epoch in range(n_epochs):
# Random shuffling
np.random.shuffle(train_total_data_normal)
train_data_ = train_total_data_normal[:, 0:x_dim]
train_label_ = train_total_data_normal[:, x_dim]
#test #################################
test_data = test_total_data[:,0:x_dim]
test_labels = test_total_data[:,x_dim]
#######################################
# Loop over all batches
for i in range(number_of_batches):
# Compute the offset of the current minibatch in the data.
offset = (i * batch_size) % (total_training_instances)
batch_x_input = train_data_[offset:(offset + batch_size), :]
_, ae_loss_val, energy_loss_val, p_sigma_loss_val, total_loss_val = sess.run(
(training_op, ae_loss, energy_loss, P_Sigma_loss, total_loss),
feed_dict={x: batch_x_input, dropout_prob : hp_drop,
dropout_prob_paper : hp_drop, training: True})
#print("epoch = ",epoch, "batch_number = ", i,
#"ae_loss=", ae_loss_val, "energy_loss=", energy_loss_val,
#"p_sigma_loss_val=", p_sigma_loss_val, "total_loss=", total_loss_val)
#evaluate energy of total training dataset each training step
energy_loss_val_entire = sess.run((energy_loss), feed_dict={x: train_data_ ,
dropout_prob : 0.0, dropout_prob_paper : 0.0, training: False} )
#print("energy loss entire batch=", energy_loss_val_entire)
'''
Training done; Start testing
TO DO
1) Calculate fixed phi, mu, and covariance derived on whole training data set
2) Define "Test_Energy" function using fixed values above in (1) and taking input points
to give Energy this can calculate energy of 1 point or a batch.
3) Use this to calaculate energy of each data point (normal and anomaly) in test dataset.
If normal/anomaly ratio is 4:1 then define an anomaly as the 80th percentile
energy threshold (find this threshold)
4) Using this threshold and entire test dataset,
calcultate predcision-recall curves, F1 score, etc...
#########################################
'''
#1)
phi_test_val, mu_test_val, cov_test_val = sess.run((phi, mu, covariance),
feed_dict={x: train_data_ , dropout_prob : 0.0,
dropout_prob_paper : 0.0, training: False} )
#2)
energy_test = test_energy(z_concat, phi_test_val , mu_test_val, cov_test_val, z_dim, K_dims)
#3)
energy_test_val = sess.run((energy_test),
feed_dict={x: test_data , dropout_prob : 0.0,
dropout_prob_paper : 0.0, training: False} )
result_val = minimize_scalar(f1, args=(energy_test_val,test_labels))
return result_val.fun #note: negative of F1-score is returnedneg_f1_score = dagmm(n_epochs=50, z_dim=1,K_dims=3,lamda1=0.1,lamda2=0.01,lr=0.0001,batch_size=1024)
print("neg F1 score result=", neg_f1_score)
#use scikit optimize (skopt) function gp_minimize to perfrom hyperparamter optimization
#import pickle
import numpy as np
import skopt
from skopt import gp_minimize
def main(params):
n_epochs, lamda1, lamda2, lr, batch_size, n_hidden1, n_hidden2, n_hidden3, n_layer1 = params
print("params:n_epochs, l1, l2, lr, batch_size, n_h1, n_h2, n_h3, n_l1 :", params)
neg_f1_score = dagmm(n_epochs=n_epochs, z_dim=1,K_dims=3,lamda1=lamda1,
lamda2=lamda2,lr=lr,batch_size=batch_size,n_hidden1=n_hidden1,
n_hidden2=n_hidden2, n_hidden3=n_hidden3, n_layer1=n_layer1)
return neg_f1_score
if __name__ == "__main__":
params = [
(7, 100),
np.logspace(-2, 0, 10),
np.logspace(-3, -1, 10),
np.logspace(-4, -1, 10),
(256, 2000),
(10, 100),
(10, 100),
(3, 10),
(5,30)
]
res = gp_minimize(func=main, dimensions=params, n_calls=300, verbose=True)
print(res.x, res.fun)
#pickle.dump(res, open('res.pkl', 'wb'))
[참고 자료]
1. 기계학습(Machine Learning) 기반 이상 탐지(Anomaly Detection) 기법 연구
연구보고서+2018-16.pdf
2. Anomaly-detection 관련 논문 서베이 github
https://github.com/hoya012/awesome-anomaly-detection
hoya012/awesome-anomaly-detection
A curated list of awesome anomaly detection resources - hoya012/awesome-anomaly-detection
github.com
'Review > 논문 리뷰' 카테고리의 다른 글
| [논문 리뷰] 정형 데이터를 위한 딥러닝 | Tabnet (1) | 2022.10.19 |
|---|---|
| [논문 리뷰] 페이스북 시계열예측 모델 | prophet (1) | 2022.10.19 |
| [논문 실습] 페이스북 시계열예측 모델 | prophet with 제주도 관광객 예측 (1) | 2022.10.19 |
| [논문 리뷰] 이미지 클러스터링 | Deep Adaptive Image Clustering(2017) (0) | 2022.10.19 |
| [논문 리뷰] Helical time representation to visualize return-periods of spatio-temporal events(2017) (0) | 2022.10.19 |