모델링의 가장 기본이 되는 선형 회귀모델을 적합할 때는 4가지 기본 가정을 만족해야 한다.
다음과 같은 회귀모델이 있다고 하면,
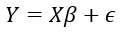
1. 선형성 : 독립변수(X)와 종속변수(Y) 간의 선형 관계 존재
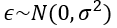
2. 독립성 : 오차항 epsilon 간 서로 독립
3. 등분산성 : 오차항 epsilon들의 분산이 일정
4. 정규성 : 오차항 epsilon은 평균이 0인 정규분포를 따름
오늘은 선형 회귀 적합시, 정규성이나 등분산성 가정을 만족하지 않는 경우 처리하는 방법에 대해 알아보려고 한다.
모델링을 할 때, 한쪽으로 쏠린 데이터나, 잔차 그래프에서 점점 분산이 커지는 것을 데이터를 만나는 경우가 많은데
이경우 적용할 수 있는 방법 중 하나가 Y를 변환해주는 것이다.
Box-Cox변환을 일반적으로 많이 사용하고 있다.

하지만 Box-Cox변환은 y가 0이거나 0보다 작은 경우는 적용할 수 없다는 한계가 있다.
이를 개선하는 방법으로 제안된 것이 Yeo-Johnson Power Transformations이다.

식을 보면 y값들이 0보다 크면 기존 y에 1을 더한 뒤, Box-Cox 변환하는 것과 일치하다.
< R코드 >
library(VGAM)
y0 = rpois(1000,0.5)+rnorm(1000,-1,0.5)
y = yeo.johnson(y = y0, lambda = 0.6)
par(mfrow=c(1,2))
plot(density(y0), main="원본 데이터 분포")
plot(density(y), main="Yeo Johnson 변환후 데이터 분포")적절한 lambda는 변환된 y를 그려보면서 정할 수 있다.

[출처] Yeo, In-Kwon; Johnson, Richard A. (2000). "A New Family of Power Transformations to Improve Normality or Symmetry". Biometrika. 87 (4): 954–959. doi:10.1093/biomet/87.4.954. JSTOR 2673623.
'Algorithm' 카테고리의 다른 글
| Tabular Data 분류, 아직도 Tree모델을 사용하고 있는 이유는?! (1) | 2024.12.16 |
|---|---|
| 추천 시스템 | TensorFlow Recommenders 리뷰 & 실습 (0) | 2023.11.14 |
| DBSCAN 차근차근 이해하기 (1) | 2022.10.19 |
| 모델 앙상블 방법 | Stacking, Blending, Voting (0) | 2022.10.19 |
| [최적해 찾기] Multiple response optimization (0) | 2022.10.19 |